Mathematics History
How Mathematics Evolved from Stone Tablets to Quantum Computing?
“Mathematics is, in its way, the poetry of logical ideas. ”
— Albert Einstein
Mathematics started with basic ideas like numbers and patterns, which are not just for humans but also found in animals. People in early societies used these concepts, like distinguishing between “one,” “two,” and “many.” The formal study of mathematics as a “demonstrative discipline” commenced in the 6th century BC with the Pythagoreans, who coined the term “mathematics” from the ancient Greek μάθημα (máthēma), meaning “subject of instruction.”

An ancient artifact called the Ishango bone, discovered near the Nile River around 20,000 years ago, consists of marks carved in three columns. Interpretations vary, with some proposing it as a tally or the earliest demonstration of prime numbers, while others suggest a six-month lunar calendar. Scholar Peter Rudman suggests that understanding prime numbers likely developed after the concept of division, dating back to around 10,000 BC, with a fuller comprehension emerging around 500 BC. The Ishango bone may have influenced later mathematical developments in Egypt, particularly in multiplication by 2, though this is debated.
Around 7,000 years ago, before ancient Egypt had its kings, people there were drawing pictures of shapes. Some folks think that in places like England and Scotland, big stone structures from about 5,000 years ago might have had shapes like circles, ellipses, and special number sets called Pythagorean triples. However, these claims are disputed, and the oldest undisputed mathematical documents come from the Babylonians (in the Middle East) and the Egyptians after they had their kings.

The roots of written math go back to the Sumerians around 3000 BC. They made a system for counting things like grain, workers, and silver. From about 2500 BC, they wrote multiplication tables, did geometry, and solved division problems. Babylonian numerals also started around then.
Babylonian mathematics used a sexagesimal (base-60) numeral system, contributing to our modern measures of time and angles. They had a place-value system, unlike the Egyptians, Greeks, and Romans. This allowed them to work with fractions easily. Despite not having a decimal point, their system was strong, giving accurate results. They introduced a zero symbol but only for certain places, not a complete place value system.

Babylonians introduced a zero symbol as a placeholder, but it was only used for intermediate positions, falling short of a true place value system. Babylonian mathematical topics included fractions, algebra, quadratic and cubic equations, calculation of regular numbers, and their reciprocal pairs. Their tablets contained multiplication tables and methods for solving linear, quadratic, and cubic equations, even featuring the earliest known statement of the Pythagorean theorem. However, similar to Egyptian mathematics, Babylonian math didn’t distinguish between exact and approximate solutions and lacked explicit statements about the need for proofs.
Archaeological findings hint that the Ancient Egyptian way of counting might have come from Sub-Saharan Africa. Some cool geometric designs they used also show up in Egyptian buildings and symbols.
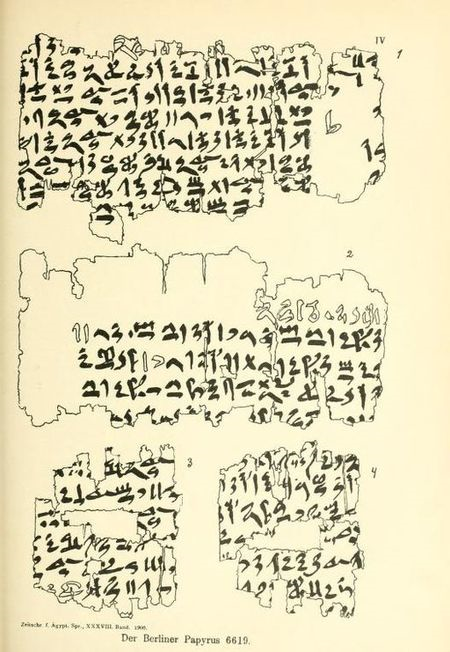
The Rhind Papyrus, a big math document, dates back to around 1650 BC. This instructional manual covers arithmetic and geometry, providing area formulas, multiplication and division methods, and insights into composite and prime numbers, as well as arithmetic and geometric series. The Moscow Papyrus, from about 1890 BC, has math problems that were probably meant for fun. One problem in there is how to find the volume of a frustum, which is like a chopped-off pyramid. Lastly, the Berlin Papyrus 6619 from around 1800 BC reveals that ancient Egyptians were capable of solving second-order algebraic equations.
Greek mathematics, from around 600 BC to 529 AD, was a big leap forward compared to earlier math. This era, known as Hellenistic mathematics after Alexander the Great, saw mathematicians residing in various cities across the Eastern Mediterranean, from Italy to North Africa, sharing a common culture and language. Unlike earlier math which relied on observations, Greek math used deductive reasoning. They employed logic to derive conclusions from definitions and axioms, emphasizing mathematical rigor in their proofs.

Thales of Miletus and Pythagoras are considered the starting points. They might have been inspired by Egyptian and Babylonian math. Thales used geometry to solve practical problems, earning recognition as the first true mathematician. Pythagoras founded the Pythagorean School, advocating the idea that mathematics governs the universe with the motto “All is number.” The Pythagoreans are credited with the first proof of the Pythagorean theorem and the proof of the existence of irrational numbers.
Plato was important for inspiring others. His school in Athens attracted top mathematicians like Eudoxus. Plato also discussed foundational aspects of mathematics and introduced the analytic method, with a formula for obtaining Pythagorean triples bearing his name. Eudoxus worked on the method of exhaustion, a bit like modern integration. Aristotle, another big name, laid the groundwork for logic.

In the 3rd century BC, the Museum of Alexandria emerged as the premier center for mathematical education and research. Euclid who taught and wrote the Elements there, created a highly influential textbook. The Elements introduced mathematical rigor through the axiomatic method, presenting a logical framework that encompassed familiar theorems of Euclidean geometry and topics such as number theory, algebra, and solid geometry. Euclid’s work remains fundamental in modern geometry education, addressing concepts like the irrationality of the square root of two and the infinitude of prime numbers. Euclid also explored various subjects beyond geometry, although only half of his writings have survived.

Archimedes, a famous mathematician from Syracuse around 287–212 BC, used a clever method to estimate the value of pi. He was considered the greatest mathematician of ancient times. Archimedes calculated the area under the arc of a parabola using an infinite series summation, a technique reminiscent of modern calculus. He showed that this method could be used to find pi with great precision. Archimedes delved into various mathematical pursuits, studying the spiral named after him, devising formulas for volumes of surfaces of revolution (paraboloid, ellipsoid, hyperboloid), and introducing a clever method of exponentiation for handling large numbers. One of his major accomplishments was determining the surface area and volume of a sphere, proving them to be 2/3 of the surface area and volume of a cylinder circumscribing the sphere.

Apollonius of Perga, who lived around 262–190 BC, made important contributions to the study of conic sections — shapes like circles, ellipses, and hyperbolas. He explained how to get these shapes by cutting a double-napped cone with a plane at different angles. Although Apollonius didn’t use coordinate geometry like we do today, his work on curves was similar to later developments in analytical geometry.

Around the same time, Eratosthenes created the Sieve of Eratosthenes to find prime numbers. The 3rd century BC is often seen as the “Golden Age” of Greek math, with advancements in pure math and the beginning of trigonometry by Hipparchus, who compiled the first known trigonometric table and introduced the systematic use of the 360-degree circle. Heron of Alexandria contributed Heron’s formula for finding the area of a scalene triangle and was the first to recognize the possibility of negative numbers possessing square roots. Menelaus of Alexandria pioneered spherical trigonometry through Menelaus’ theorem. The Almagest of Ptolemy, an astronomical treatise, contained trigonometric tables used by astronomers for the next thousand years. Ptolemy is also credited with Ptolemy’s theorem, deriving trigonometric quantities, and providing one of the most accurate values of π outside of China until the medieval period (3.1416).

Following a period of stagnation after Ptolemy, the era between 250 and 350 AD is sometimes referred to as the Silver Age of Greek mathematics. During this time, Diophantus made significant advances in algebra, particularly in indeterminate analysis or Diophantine analysis. The study of Diophantine equations and Diophantine approximations remains a significant area of research today. Diophantus’ major work, the “Arithmetica,” comprised 150 algebraic problems dealing with exact solutions to determinate and indeterminate equations. His work, the “Arithmetica,” became influential, inspiring mathematicians like Pierre de Fermat, who later worked on famous problems like Fermat’s Last Theorem.
Pappus of Alexandria, a mathematician from the 4th century AD, contributed to the study of conic sections. His “Collection” is an essential source for Greek mathematics. The last significant female mathematician from this era was Hypatia of Alexandria.

Hypatia of Alexandria (AD 350–415) was the first recorded woman mathematician. She followed her father, Theon of Alexandria, as the Librarian at the Great Library and wrote many works on applied mathematics. Unfortunately, due to a political disagreement, the Christian community in Alexandria publicly stripped and executed Hypatia. While her death is sometimes seen as the end of Alexandrian Greek mathematics, work continued in Athens for another century with figures like Proclus, Simplicius, and Eutocius. Although Proclus and Simplicius were more into philosophy than mathematics, their commentaries on earlier works offer valuable insights into Greek mathematics.
While Greeks kept doing math in Rome, Romans didn’t have many famous math folks. People like Cicero thought Romans preferred practical math over the fancy Greek stuff. We’re not sure if the Romans got their numbers from the Greeks or the Etruscans in Italy.
Romans were good at using math to catch financial cheats and handle taxes. Siculus Flaccus, a Roman land surveyor, wrote about measuring land areas. Romans also used math for building stuff like bridges, roads, and military plans. They even applied it to arts like mosaic-making, inspired by the Greeks. Romans needed math for their calendar. The first one had 356 days and a leap year every two years. They later fixed it with the Julian calendar by Julius Caesar. Pope Gregory XIII tweaked it more for the modern calendar we use today.
Around the same time, the Chinese and Romans both made a device to measure distances called an odometer. Vitruvius, a Roman engineer, described one with wheels and gears. It got lost but popped up again in Europe during experiments in the 15th century. The Roman odometer used wheels, gears, and dropping pebbles to measure distances.
Early Chinese math was unique compared to other places. The oldest Chinese math text, the Zhoubi Suanjing, is from around 300 BC, but there’s an even older document with a multiplication table from 305 BC. Chinese math used a cool system called “rod numerals” that worked with an abacus. This system was way ahead of its time, even before the Indian one. In 212 BC, some books got burned, so we didn’t know much about Chinese math before that. But during the Han dynasty, they wrote “The Nine Chapters on the Mathematical Art,” covering lots of stuff like farming, geometry for pagoda towers, and proving the Pythagorean theorem.
The best Chinese math happened in the 13th century with algebra. Zhu Shijie’s “Precious Mirror of the Four Elements” was a big deal, solving tricky equations. After that, Chinese math slowed down while Europe’s took off. Jesuit missionaries brought math ideas between Europe and China from the 16th to 18th centuries, but more ideas went into China than out.
Japan, Korea, and Vietnam got their math vibes from China. Korean and Japanese math liked China’s Song Dynasty, and Vietnamese math liked China’s Ming Dynasty. They all followed China’s style, presenting problems with solutions. In Korea and Vietnam, math was linked to the government, while in Japan, it was in private schools.
The first big civilization in India was the Indus Valley, around 2600 to 1900 BC. They planned their cities well, but we don’t have any math records from them. The oldest Indian math records are the Sulba Sutras, from between the 8th century BC and the 2nd century AD. These are like extra rules in religious texts for making different-shaped altars. Just like in Egypt, they linked math with religious stuff. The Sulba Sutras have ways to make a circle almost as big as a square, rough values for π, the square root of 2, Pythagorean triples, and the Pythagorean theorem. They got some ideas from Babylonian math. Like in China, Indian math has times of big progress and then quiet times.

Pāṇini (around the 5th century BC) made rules for Sanskrit grammar, kind of like how we write math today. Pingala (around the 3rd–1st centuries BC) used a thing like binary numbers and talked about combinatorics, which is like a simple version of the binomial theorem. Later, in the 4th and 5th centuries AD, there were the Siddhantas, astronomy texts with a bit of Greek influence. They introduced trigonometry based on the half-chord, not the full chord like before.
Around 500 AD, Aryabhata wrote the Aryabhatiya. It’s a short book in verse, not very organized, but it introduced the decimal place-value system. A few centuries later, Brahmagupta explained zero and how it’s a placeholder in numbers. This was part of the Hindu–Arabic numeral system that spread to Europe through Islamic scholars by the 12th century.
In the 12th century, Bhāskara II in southern India wrote a lot about different math things. He talked about tiny things, averages, and how sine works. In the 14th century, Madhava of Sangamagrama found a series for π and other things. Later, in the 16th century, Jyesthadeva put together the ideas from the Kerala School of Mathematics, and some people think these ideas went to Europe through Jesuit missionaries and traders. However some people argue that the Kerala School didn’t really have a full system for differentiation and integration, and there’s no proof their ideas went outside Kerala.
Inthe 8th century, the Islamic Empire in the Middle East, Central Asia, North Africa, Iberia, and parts of India made important contributions to math. Although most math texts were in Arabic, not all were written by Arabs.

In the 9th century, the mathematician Muḥammad ibn Mūsā al-Khwārizmī made significant contributions, writing about Hindu–Arabic numerals and methods for solving equations. His works, especially “On the Calculation with Hindu Numerals,” spread Indian mathematics to the West. The term “algorithm” comes from the Latinization of his name, and “algebra” from the title of one of his works. Al-Khwārizmī explained algebraic solutions for quadratic equations and introduced algebra for its own sake.

In Egypt, Abu Kamil took algebra further, including irrational numbers, and solved three non-linear simultaneous equations with three unknowns. His works laid the foundation for later math. Al-Karaji furthered algebra in his treatise al-Fakhri, incorporating integer powers and roots. He provided something akin to a proof by mathematical induction and discussed the binomial theorem, Pascal’s triangle, and the sum of integral cubes. In the 10th century, Abul Wafa translated Diophantus’s works into Arabic. Ibn al-Haytham found the formula for the sum of fourth powers and did integrations for polynomial volumes.
In the late 11th century, Omar Khayyam wrote about flaws in Euclid’s math, solved cubic equations, and influenced calendars. In the 13th century, Nasir al-Din Tusi advanced spherical trigonometry, and in the 15th century, Ghiyath al-Kashi calculated π and worked on roots. Muslim mathematicians also introduced the decimal point, discovered trigonometric functions, and developed algebraic geometry. However, math progress slowed during the Ottoman and Safavid Empires from the 15th century.
Inthe 17th century, a lot of cool math and science stuff happened in Europe. Galileo used a telescope to check out Jupiter’s moons, and Tycho Brahe collected tons of data on where planets were in the sky. Johannes Kepler, who worked with Brahe, figured out how planets move. Thanks to John Napier and Jost Bürgi inventing logarithms, Kepler’s math got easier. René Descartes’ analytic geometry, developed between 1596 and 1650, allowed for the plotting of these orbits on graphs using Cartesian coordinates.
Isaac Newton built on this work and discovered the laws of physics that explain how planets move, and he also came up with calculus. At the same time, Gottfried Wilhelm Leibniz independently developed calculus and contributed to the binary number system, foundational for modern computers, including the Von Neumann architecture. Leibniz is often regarded as the founder of computer science.
In addition to space studies, math started getting used in new ways. Pierre de Fermat and Blaise Pascal began thinking about probability and combinatorics during a gambling game. Pascal, with his famous wager, tried using probability to argue for religious life, saying that even if the chances were slim, the rewards were huge. This foresaw the development of utility theory in the 18th–19th century.

Leonhard Euler, born in 1707, stands out as the most influential mathematician of the 18th century. His impact is vast, from pioneering graph theory with the Seven Bridges of Königsberg problem to standardizing modern mathematical terms and notations. Euler introduced the symbol “i” for the square root of minus 1 and popularized using the Greek letter “π” for the ratio of a circle’s circumference to its diameter. His extensive contributions spanned topology, graph theory, calculus, combinatorics, and complex analysis, evident in the many theorems and notations named after him.
Another notable mathematician of the 18th century was Joseph Louis Lagrange, known for groundbreaking work in number theory, algebra, differential calculus, and the calculus of variations. Pierre-Simon Laplace, during the Napoleon era, made significant contributions to the foundations of celestial mechanics and statistics.

In the 19th century, math got more abstract. Carl Friedrich Gauss did awesome stuff in complex variables, geometry, and series. He also proved the fundamental theorem of algebra and the quadratic reciprocity law. The century witnessed the development of non-Euclidean geometry by mathematicians Nikolai Ivanovich Lobachevsky, János Bolyai, and Bernhard Riemann. Hyperbolic geometry, where the uniqueness of parallels no longer holds, and elliptic geometry, where no parallels can be found, challenged traditional notions. Riemann’s work also extended to Riemannian geometry, unifying and generalizing the three types of geometry, laying the foundation for the theory of general relativity.
Abstract algebra emerged, with Hermann Grassmann introducing vector spaces, William Rowan Hamilton developing noncommutative algebra, and George Boole creating Boolean algebra, a fundamental concept in mathematical logic, electrical engineering, and computer science. Mathematicians such as Augustin-Louis Cauchy, Bernhard Riemann, and Karl Weierstrass redefined calculus more rigorously.
Niels Henrik Abel and Évariste Galois explored the limits of mathematics, proving the impossibility of a general algebraic method for solving polynomial equations of degree greater than four (Abel–Ruffini theorem). Their work laid the foundation for group theory and abstract algebra, central to the study of symmetry in the 20th century. Georg Cantor created set theory, changing how we think about infinity. Mathematicians like Peano, Hilbert, and Russell sparked debates on the foundations of math.


In the 20th century, math became a major field with many new Ph. D.s and job opportunities. In 1900, David Hilbert outlined 23 unsolved math problems. Over the century, 10 were solved, 7 partially, and 2 remain open. 4 are too vaguely stated. Big historical questions got answers. The four-color theorem was proven in 1976 by Wolfgang Haken and Kenneth Appel, though controversial for computer use. Andrew Wiles proved Fermat’s Last Theorem in 1995, and Paul Cohen and Kurt Gödel demonstrated the independence of the continuum hypothesis from the standard axioms of set theory. Massive math collaborations happened, like the extensive proof for finite simple groups from 1955 to 2004. The “Nicolas Bourbaki” group tried to explain all math as a unified whole, but it stirred controversy in education.
Mathematics underwent significant growth during the 20th century. Albert Einstein used math in new ways, especially in his theory of relativity. New areas like mathematical logic and topology came up, and John von Neumann’s game theory changed how we solve problems. We started using abstract structures, like metric and topological spaces. Mathematicians got creative, leading to category theory. Algebraic geometry got a makeover with sheaf theory. We made progress in dynamical systems, measure theory, and knot theory. Quantum mechanics led to functional analysis.
Abraham Robinson brought back infinitesimal calculus with non-standard analysis. John Horton Conway discovered surreal numbers related to games. Computers got better, transforming industries. Math adapted with Alan Turing’s computability theory and complexity theory. Discrete concepts, combinatorics, and graph theory became more important with computers. We tackled big problems with algorithms like the simplex algorithm, fast Fourier transform, and RSA for encryption.
We also realized math has limits. In 1929–1930, we figured out what’s true or false about natural numbers with addition or multiplication. But Kurt Gödel showed in 1931 that we can’t figure out everything. Even David Hilbert’s dream of a complete and consistent math system had to change. Some mathematicians in the 20th century were Srinivasa Aiyangar Ramanujan, who made over 3000 theorems, and Paul Erdős, who worked with many others. Emmy Noether made important contributions to ring, field, and algebra theories.
“Math is the language of the universe. So the more equations you know, the more you can converse with the cosmos.”
— Neil deGrasse Tyson
Thank you for reading this story and see you again. If you’d like to show your appreciation, please give the claps and leave a response.
If you like my work and wanna support me, you can buy me a coffee ☕️. If you do so, thank you a million times. 🙂